動點的軌跡在機械構造設計上也有很多的應用,透過電腦的模擬,事先了解機械元件行程的範圍,可以避免元件之間干涉的情形發生。
今天要介紹四連桿機構(four-link-mechanism)中的曲柄搖桿機構(crank-rocker-mechanism),因為本人不是機械專長,主要是以運動軌跡的角度加以介紹並製作輔助教學網頁,如果有錯誤的部分,再麻煩加以指正。
下圖是曲柄搖桿機構的示意圖。
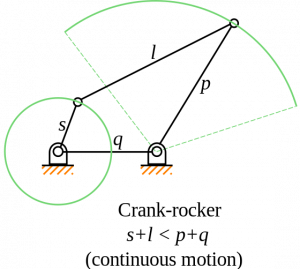
圖片來源:https://engineering.stackexchange.com/questions/45230/is-there-a-formula-that-relates-the-two-angles-in-a-crank-rocker
圖中,q為機架或連心線、s為曲柄,可以繞軸三百六十度轉動,為主動連桿,l為浮桿或稱連接桿,而p則為搖桿,只能做擺動運動。
當l和s成一直線時,會構成兩個死點,依三角形兩邊和大於第三邊可以得到p+q>l+s和p-q<l-s即p+s>l+q
曲柄搖桿機構的作圖並不困難。
const q = 8, s = 2, p = 4.5
const l = Math.sqrt(p * p + q * q - s * s)
const pointA = board1.create('point', [-4, 0])
const pointB = board1.create('point', [() => pointA.X() + q, 0])
const dead1OfC = { x: pointA.X() + s * Math.cos(theta1), y: pointA.Y() + s * Math.sin(theta1) }
const dead2OfC = { x: pointA.X() + s * Math.cos(theta2), y: pointA.Y() + s * Math.sin(theta2) }
const circleC1 = board1.create('circle', [pointA, () => s], { visible: false })
const circleC2 = board1.create('circle', [pointB, () => p], { visible: false })
const pointC = board1.create('glider', [-2, 0, circleC1])
const circleC3 = board1.create('circle', [pointC, () => l], { visible: false })
const pointD = board1.create('intersection', [circleC2, circleC3], { visible: false })
l的計算主要是為了讓搖桿左右對稱搖擺。
我們做了四個按鈕,進行模擬的控制。
<button class="btn startAnimation">開始模擬</button>
<button class="btn stopAnimation">停止模擬</button>
<button class="btn goToDead1">前往死點1</button>
<button class="btn goToDead2">前往死點2</button>
前往第1死點和前往第2死點需計算C點的位置,先用餘弦定理計算角度,再將極坐標轉換到直角坐標算出位置。
const theta1 = Math.acos((Math.pow(l + s, 2) + q * q - p * p) / (2 * (s + l) * q))
const theta2 = Math.acos((Math.pow(l - s, 2) + q * q - p * p) / (2 * (l - s) * q)) + Math.PI
const dead1OfC = { x: pointA.X() + s * Math.cos(theta1), y: pointA.Y() + s * Math.sin(theta1) }
const dead2OfC = { x: pointA.X() + s * Math.cos(theta2), y: pointA.Y() + s * Math.sin(theta2) }
const startAnimation = document.querySelector('.startAnimation')
const stopAnimation = document.querySelector('.stopAnimation')
const goToDead1 = document.querySelector('.goToDead1')
const goToDead2 = document.querySelector('.goToDead2')
startAnimation.addEventListener('click', () => {
pointC.startAnimation(1, 1000, 0)
})
stopAnimation.addEventListener('click', () => {
pointC.stopAnimation()
})
goToDead1.addEventListener('click', () => {
pointC.stopAnimation()
pointC.moveTo([dead1OfC.x, dead1OfC.y], 1000)
})
goToDead2.addEventListener('click', () => {
pointC.stopAnimation()
pointC.moveTo([dead2OfC.x, dead2OfC.y], 1000)
})
startAnimation(方向,步驟數,遞延時間),moveTo(位置,執行時間)
執行畫面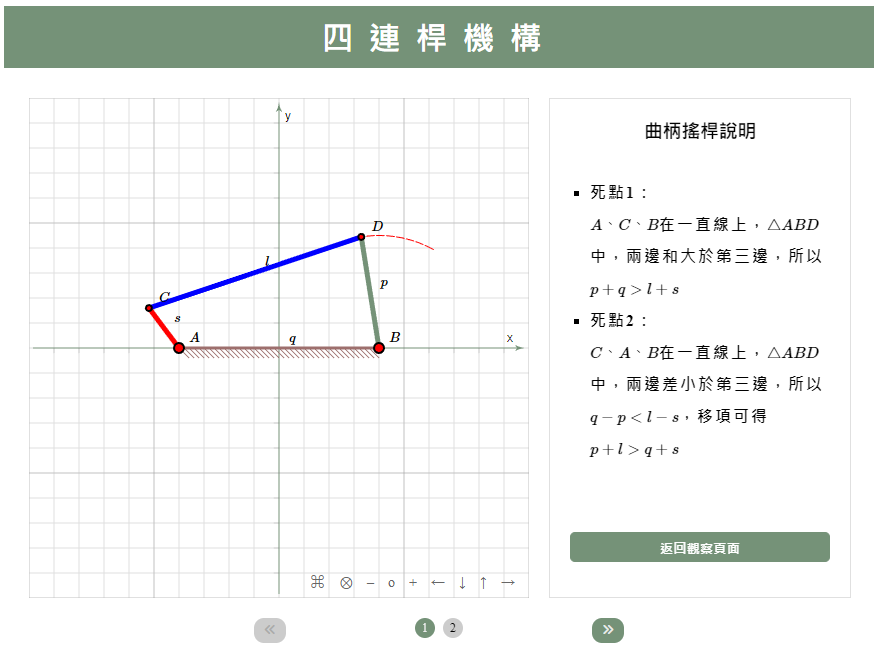
除了曲柄搖桿機構外,四連桿機構還有雙曲柄機構、雙搖桿機構、滑塊曲柄機構...等,有興趣的朋友可以加以補充,也可以對機械設計有些認識。因為時間的壓力,網頁還有些細節可以加強,教學的補分也可以再發揮。
很多學生都不喜歡數學,甚至抱著「數學無用論」的觀念,從今天的例子可以看出來,在理工的領域,無處不需要數學的知識,所以事實是「數學不是沒有用,而是你不會用。」台灣是科技立國,理工人材很是欠缺,而理工的基礎又是數學,希望透過好的數學教學媒體,能夠激發更多人學好數學。
